Hey there. If you need to find how far apart two points are on a graph, the distance formula is your friend. It comes from basic math you already know. In this guide, I’ll show you what it is, how to use it, and more. You’ll get examples, tips, and even some real-world ideas. Let’s make this easy.
What Is the Distance Formula?
The distance formula helps you measure the straight line between two points on a plane. Think of it as a quick way to get the length without drawing lines each time.
The formula looks like this:
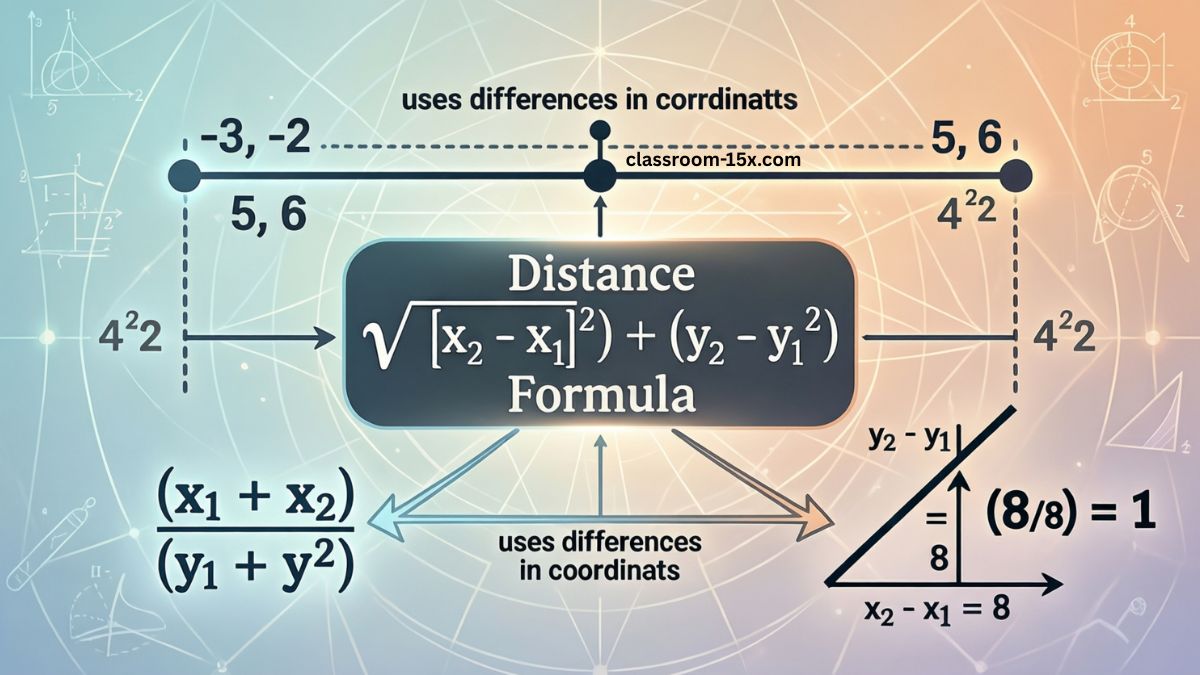
Distance = √[(x₂ – x₁)² + (y₂ – y₁)²]
Here, (x₁, y₁) is your first point. (x₂, y₂) is the second. The square root covers the whole thing inside. Don’t worry about the order of points. It won’t change the answer.
This works for any two points. You plug in the numbers and calculate.
How Does the Distance Formula Come From?
It starts with the Pythagorean theorem. You know, a² + b² = c² for right triangles.
Picture two points on a graph. Draw a line between them. Now add lines along the x and y axes to make a right triangle.
The base is the difference in x values: |x₂ – x₁|.
The height is the difference in y values: |y₂ – y₁|.
The slant side is the distance. So, distance² = (x difference)² + (y difference)².
Take the square root to get the distance. That’s it. Simple, right?
Step-by-Step Examples of the Distance Formula

Let’s try some problems. I’ll walk you through each one.
Basic Example: Two Simple Points
Find the distance between (5, 1) and (1, -2).
First, subtract x values: 1 – 5 = -4.
Subtract y values: -2 – 1 = -3.
Square them: (-4)² = 16, (-3)² = 9.
Add: 16 + 9 = 25.
Square root: √25 = 5.
So, the distance is 5 units.
Example: Find the Radius of a Circle
Say the center is at (3, -1). A point on the edge is (7, 3).
Use the formula: √[(7 – 3)² + (3 – (-1))²] = √[4² + 4²] = √[16 + 16] = √32 = 4√2.
That’s about 5.66 if you round. But keep it exact when you can.
Example: Points at a Set Distance
You want points 5 units from (3, 4) on the line x = 7.
Set up: √[(7 – 3)² + (y – 4)²] = 5.
Square both sides: 16 + (y – 4)² = 25.
Then (y – 4)² = 9.
So y – 4 = 3 or -3.
Y = 7 or 1.
Points are (7, 7) and (7, 1).
Example: Points with Fractions
Try (-1/2, 3) and (3/2, -1).
X diff: 3/2 – (-1/2) = 2.
Y diff: -1 – 3 = -4.
Squares: 4 + 16 = 20.
√20 = 2√5.
About 4.47.
See? It handles fractions too.
Common Mistakes to Avoid with the Distance Formula
We all mess up sometimes. Here are big ones to watch.
- Mix up x and y. Always subtract x from x, y from y.
- Forget the square root. You end up with distance squared.
- Wrong order inside. Do subtract first, then square.
- Use wrong signs. But squares fix negatives anyway.
- Round too soon. Stay exact till the end.
Fix these, and you’ll be good.
Read: Year of the Snake Google Game 2026: Play Tips, Strategies, and Hidden Meanings
The Distance Formula in 3D Space
What if points are in space? Add a z axis.
The formula grows: √[(x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)²].
Example: (1, 2, 3) to (4, 6, 0).
Diffs: 3, 4, -3.
Squares: 9 + 16 + 9 = 34.
√34 ≈ 5.83.
Use this for 3D games or maps.
Real-Life Uses of the Distance Formula
Math isn’t just school. It shows up everywhere.
- In GPS: Your phone finds distance to spots.
- Sports: Golfers calculate shot lengths.
- Building: Engineers measure beam spans.
- Games: Video games track character moves.
- Maps: Find shortest path between cities.
Next time you use a map app, think of this formula at work.
How the Distance Formula Links to Other Math
It ties into more stuff.
With the Midpoint Formula
Midpoint splits a line in half. Formula: ((x₁ + x₂)/2, (y₁ + y₂)/2).
The distance from midpoint to each end should be half the full distance.
Example: From earlier, (-3, -2) to (5, 6). Midpoint (1, 2).
Full distance 8√2. Half is 4√2 each way. It checks out.
With Slope and Lines
Slope is rise over run: (y₂ – y₁)/(x₂ – x₁).
Distance uses those diffs squared.
Together, they help graph lines and find lengths.
Practice Problems to Try
Here’s a table with problems. Try them, then check answers.
| Problem | Points | Your Answer | Solution |
|---|---|---|---|
| 1 | (0, 0) and (3, 4) | √(9 + 16) = 5 | |
| 2 | (2, 5) and (-2, -5) | √(16 + 100) = √116 = 2√29 ≈ 10.77 | |
| 3 | (1, 1, 1) and (2, 3, 5) (3D) | √(1 + 4 + 16) = √21 ≈ 4.58 | |
| 4 | Center (0,0), point (5,12). Radius? | √(25 + 144) = 13 |
Work through these. They build skill.
Conclusion
The distance formula — √[(x₂ − x₁)² + (y₂ − y₁)²] — is one of the easiest and most useful tools in math, letting you find the straight-line distance between any two points on a plane (and even in 3D with one extra term). Rooted in the Pythagorean theorem, it helps with everything from basic geometry problems and circle equations to real-life applications like maps, games, and GPS. Once you practice a few examples and watch out for simple mistakes like skipping the square root, it becomes second nature — a skill you’ll carry through school, exams, and beyond. Keep using it, and you’ll see just how powerful one little formula can be!
Frequently Asked Questions
What if the points are the same?
Distance is zero. Plug in, get √0 = 0.
Does order matter in the formula?
No. Switch points, diffs change sign, but squares stay the same.
Can I use this for more than two dimensions?
Yes. Add more terms for higher dimensions.
What’s the difference between distance and displacement?
Distance is length. Displacement adds direction, like a vector.
How do I calculate distance on a sphere, like Earth?
That’s great circle distance. Different formula for curves.
Why keep answers exact?
Exact is precise. Rounding can add errors.
Is there a distance formula for time or speed?
Yes, d = rt for motion. But that’s not coordinates.



