Kinematic equations help you understand how things move. You can use them to find how fast something goes, how far it moves, or how long it takes to get somewhere. These equations only work when the object speeds up or slows down at a steady rate.
In this guide, you’ll learn what each equation means, how to use it, and what mistakes to avoid. You’ll also see real examples to help you practice.
What Are Kinematic Equations?
Kinematic equations use five parts of motion:
- Displacement (s) – how far something moves
- Initial velocity (u) – how fast it starts
- Final velocity (v) – how fast it ends
- Acceleration (a) – how fast the speed changes
- Time (t) – how long it moves
If you know any three of these, you can find the rest.
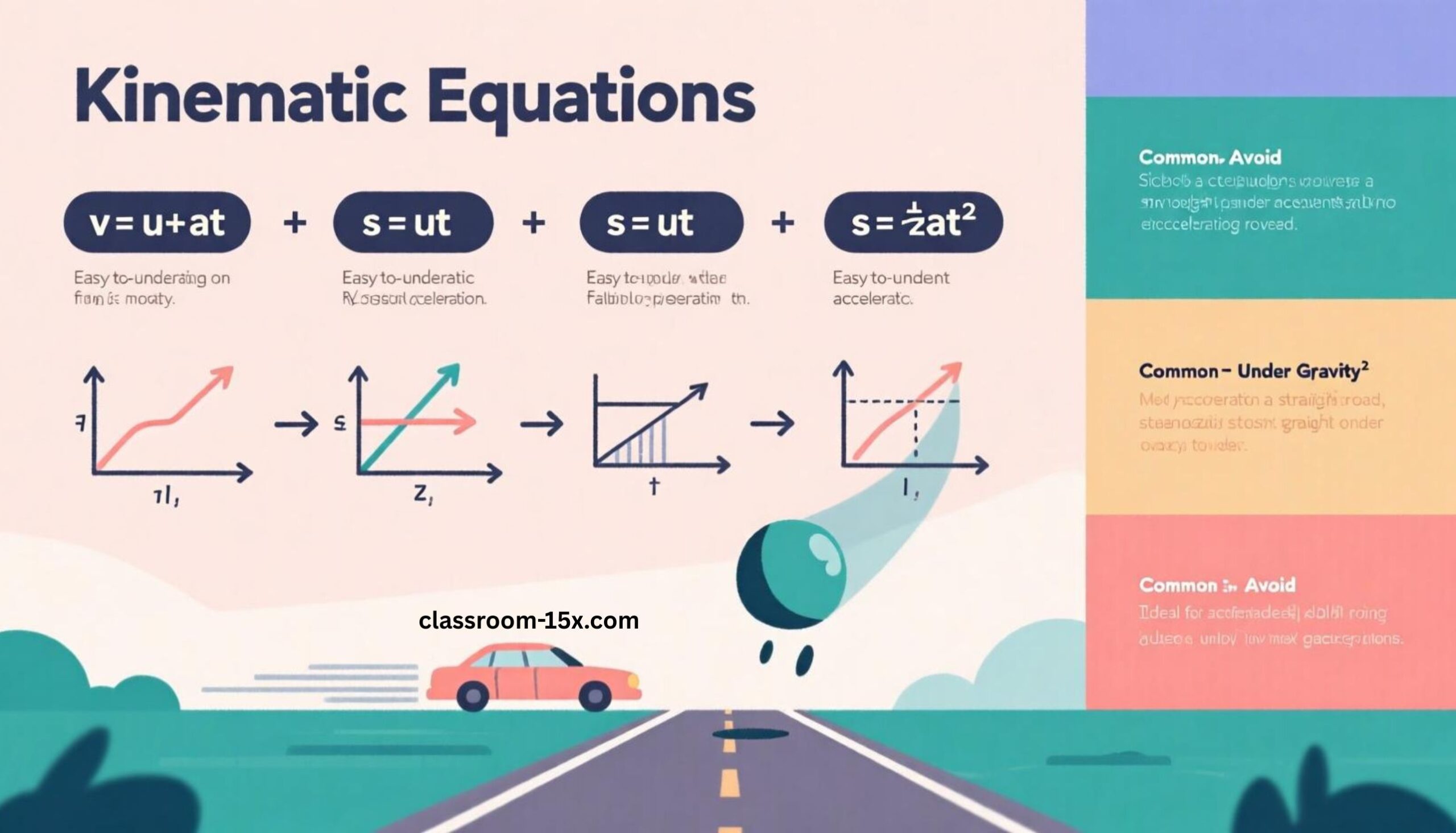
Here are the four main kinematic equations:
- v = u + at
- s = ut + ½at²
- v² = u² + 2as
- s = ½(u + v)t
You do not need to use all four at once. Choose the one that fits your problem.
When Can You Use These Equations?
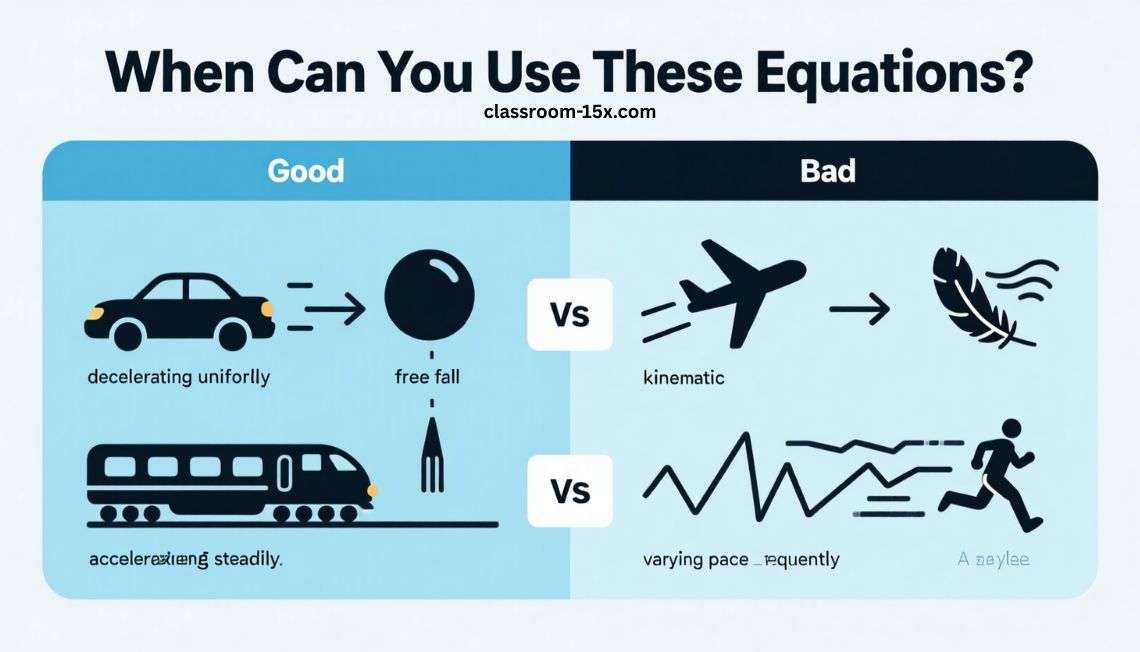
You can use kinematic equations when:
- The object moves in a straight line
- The acceleration stays the same
- The forces acting on the object do not change
Good examples:
- A car slows down evenly
- A ball falls straight down
- A train speeds up at the same rate
Bad examples:
- A plane changing speed and direction often
- A feather falling through the wind
- A runner who speeds up and slows down a lot
If the speed keeps changing in strange ways, these equations will not work.
What Each Equation Does
Each equation helps you solve for a different thing. Use what you already know to pick the right one.
1. v = u + at
Use this when you want to find how fast something is going at the end.
You need:
- Starting speed (u)
- Acceleration (a)
- Time (t)
Example:
A bike starts at 5 m/s and speeds up at 3 m/s² for 4 seconds.
v = 5 + (3 × 4) = 17 m/s
2. s = ut + ½at²
Use this when you want to find out how far something goes.
You need:
- Starting speed (u)
- Time (t)
- Acceleration (a)
Example:
A ball starts from rest (u = 0) and accelerates at 2 m/s² for 5 seconds.
s = 0 + ½(2)(25) = 25 meters
3. v² = u² + 2as
Use this when you want to find speed or distance but do not know time.
You need:
- Starting speed (u)
- Acceleration (a)
- Distance (s)
Example:
A scooter starts at 6 m/s and moves 30 meters with an acceleration of 2 m/s².
v² = 36 + 2(2)(30) = 36 + 120 = 156
v = √156 ≈ 12.5 m/s
4. s = ½(u + v)t
Use this when you know the starting and ending speeds and want to find the distance.
You need:
- Starting speed (u)
- Final speed (v)
- Time (t)
Example:
A car goes from 8 m/s to 16 m/s in 4 seconds.
s = ½(8 + 16)(4) = 48 meters
Steps to Solve a Kinematic Problem
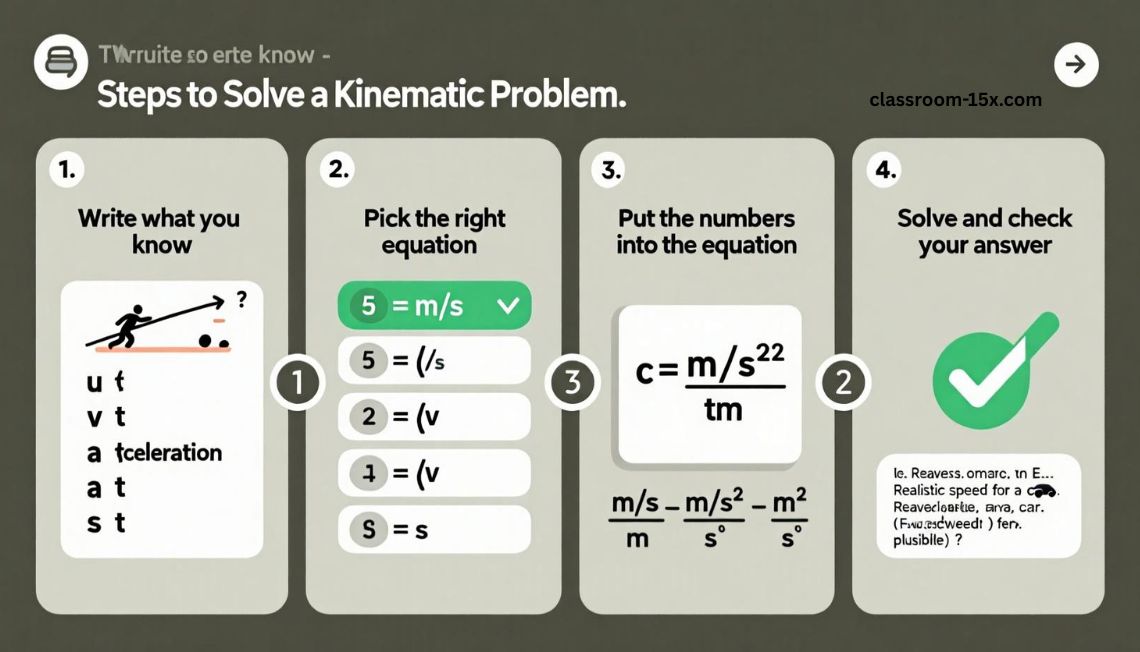
- Write what you know
List u, v, a, s, and t. - Pick the right equation
Choose the one with the unknown you want and the knowns you have. - Put the numbers into the equation
Make sure the units match. Use seconds, meters, etc. - Solve and check your answer
Make sure the result makes sense.
Real Example: Falling Object
Problem: A rock drops from a cliff that is 45 meters high. How long does it take to hit the ground?
You know:
- u = 0 (starts at rest)
- a = 9.8 m/s² (gravity)
- s = 45
- t = ?
Use: s = ut + ½at²
Plug in the numbers:
45 = 0 + ½(9.8)t²
45 = 4.9t²
t² = 45 ÷ 4.9 ≈ 9.18
t = √9.18 ≈ 3.03 seconds
Answer: The rock hits the ground after about 3 seconds.
Common Mistakes to Watch For

1. Choosing the wrong formula
Make sure the formula includes the parts you know and the one you need.
2. Mixing units
Keep units the same. Use meters and seconds together. Don’t mix meters with kilometers or seconds with minutes.
3. Forgetting signs
Direction matters. If something goes down, use a negative sign if up is positive. Be careful with acceleration too.
4. Assuming values
Don’t guess. Only use a value if the question gives it to you or if it’s common knowledge, like gravity.
Why These Equations Matter
You’ll see kinematic equations in school, on tests, and in labs. But they also matter outside of class. Engineers use them to build machines and roads. Pilots use them when taking off and landing. Athletes use them to understand motion.
If you want to study physics, these equations are a must. They help you solve problems by breaking them into steps.
Read: Physics Classroom: What Happens, What You Learn, and Why It Matters
Extra Tips
- Gravity pulls things down at 9.8 m/s²
- If something moves in a straight line, use these equations
- Always write out what you know before solving
- Draw a simple picture if that helps
FAQs
Q: Do I need to learn all four equations?
Yes. But more than that, you should know how to choose the right one for each problem.
Q: What if the acceleration changes?
Then these equations do not work. You’ll need more advanced tools, like calculus.
Q: Can I use these for up-and-down motion?
Yes. Just make sure you treat gravity as negative if up is your positive direction.
Q: What if the object is not moving at the start?
Then the initial velocity (u) is zero. That makes some equations easier.
Q: What does a negative answer mean?
It means the object went in the opposite direction of what you called positive.
Conclusion
Kinematic equations help you find how something moves when the acceleration stays the same. Use them to solve for speed, time, or distance.
Here are the four again:
- v = u + at
- s = ut + ½at²
- v² = u² + 2as
- s = ½(u + v)t
To solve any problem:
- Write what you know
- Pick the right equation
- Plug in the numbers
- Solve and check your units
With practice, these problems get easier. These equations help you understand real motion. And once you understand motion, you can understand the world around you.